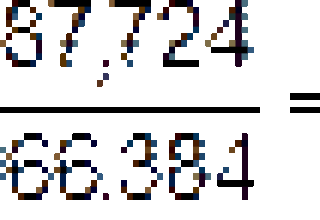Практическое занятие 2 расчет средних величин
Практические занятия № 5. Расчет средних величин
Цели занятия:
· обобщение и систематизация материала по теме
· сформировать умения: собрать и регистрировать статистическую информацию ;
· развитие общих компетенций по
· ОК 2. Анализировать социально-экономические и политические проблемы и процессы, использовать методы гуманитарно-социологических наук в различных видах профессиональной и социальной деятельности.
· ОК 3. Организовывать свою собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество
· ОК 5. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
· Форма организации занятия– индивидуальная
Студент должен
· Предмет, методы и задачи статистической науки
· Общие основы статистической науки
· Принципы организации государственной статистики
· Основные способы сбора, обработки, анализа и наглядного представления информации
· Технику расчета статистических показателей, характеризующих социально-экономические явления
Вопросы для проверки готовности студентов к практическому занятию
· Средняя величина в статистике. Значение, практическое применение
· От чего зависит выбор вида средней величины
· Средняя величина дискретного ряда.
· Средняя геометрическая величина, условия применения
· Средняя хронологическая величина, ее применение и практическое использование
Форма отчетности по занятию: письменное решение задач в тетради для практических работ
Задача 1.Результаты работы страховых организаций за 9 мес. 2015 г. характеризуются нижеприведенными данными.
| Организация | Страховой взнос V, млн. руб. | Коэффициент выплат Кв | Выплаты W=Kв∙V, млн. руб. |
| Росгосстрах | 3706,420 | 0,37 | 1351,055 |
| Ресо Гарантия | 75,715 | 1,08 | 81,868 |
| Альфа страхование | 184.249 | 0,30 | 54,801 |
| Итого | 3966,384 | – | 1487,724 |
1) средний коэффициент выплат;
2) абсолютную сумму дохода страховых организаций;
Решение:
1. Рассчитаем средний коэффициент выплат с помощью средней арифметической:
2. Абсолютная сумма дохода страховых организаций:
Δ = V – W = 3966,384 –1487,724 = 2478,660 млн. руб.
Задача 2.В страховой компании, состоящей из трех подразделений, проводится исследование по стажу работы. Результаты обследований приведены в таблице
| Стаж работы (лет) | До 5 | 5 — 15 | 15 — 25 | Свыше 25 |
| № подраздел. | ||||
| I | ||||
| II | ||||
| III |
Оцените средний уровень стажа в каждом подразделении и по всей фирме в целом; проведите сравнение общего среднего стажа по подразделениям со средним стажем по фирме в целом. Сделайте выводы.
Решение:
Перейдем от вариационного ряда к моментному. Для этого найдем среднее у закрытых интервалов. Оно равно 5. Исходя из этого, строим точечный ряд.
| № стаж работы | Всего |
| Всего |
1. Средний стаж на каждом подразделении: (средняя взвешенная арифметическая)
На первом подразделении: = (2*0 + 10*5 + 20*20 + 30*10) / 37 = 20,27
На втором подразделении: = (10*0 + 10*20 + 10*20 + 15*30) / 55 = 15,455
На третьем подразделении: = (3*0 + 10*10 + 30*20 + 30*5) / 48 = 17,708
2. Средний стаж на фирме = (0*15 + 35*10 + 60*20 + 30*30) / 140 = 17,5
3. Средний стаж по подразделениям:
4. Сравнение средних стажей по подразделениям между собой:
Выводы:
·На первом подразделении средний стаж работы больше, чем на втором на 5,315 лет, чем на третьем на 2,562 года. На третьем подразделении больше, чем на втором на 2,253 года.
·Сравнение общего среднего стажа по подразделениям со средним стажем по фирме в целом: эти стажи практически равны, хотя теоретически они должны быть равны.
Задача 3. Имеются следующие данные о возрастном составе студентов группы заочного отделения ВУЗа (лет): 19; 19; 19; 20; 20; 20; 20; 20; 20; 20; 20; 20; 21; 21; 21; 22; 23; 23; 24; 25; 25; 25; 26; 27; 29. Рассчитать средний возраст студентов.
Решение: расчет проводится по средней арифметической взвешенной:
где а-варианта (признак. возраст), а f-частота, число повторений признака
Задания для самостоятельного решения
Задача 1. Вычислите среднемесячную заработную плату рабочих по организации в целом на основании следующих данных:
| Наименование цеха | Количество рабочих, чел. | Средняя заработная плата, руб. |
| Хлебобулочный | ||
| Кондитерский | ||
| Безалкогольных напитков |
Укажите вид применяемых средних величин, напишите и обоснуйте формулу.
Задача 2.Определите среднюю цену реализации свежих огурцов на основании следующих данных:
| Месяцы | Цена за 1 кг | Продано, кг |
| апрель | 80,0 | |
| май | 75,0 | |
| июнь | 64,0 |
Укажите вид применяемой средней величины, напишите формулу.
Задача 3 .Рассчитайте средний стаж работы страховщика на основании следующих данных:
| Стаж работы, лет | Численность работников, чел. |
Укажите вид применяемой средней величины, напишите вывод.
Методическая разработка практического занятия по дисциплине «Статистика» на тему «Расчет средних величин и показателей вариации» (2 курс)
Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .
Курс повышения квалификации за 340 рублей!
Эмоциональное выгорание педагогов. Профилактика и способы преодоления
Методическая разработка практического занятия
по дисциплине «Статистика» на тему
«Расчет средних величин и показателей вариации»
для студентов СПО специальностей: 120714 «Земельно-имущественные отношения», 030912 «Право и организация социального обеспечения» и 080214 «Операционная деятельность в логистике»
Автор: преподаватель специальных
экономических дисциплин О.В. Антонова
Тема: Расчет средних величин и показателей вариации
Цель: научить находить различные средние величины и показатели вариации: среднюю арифметическую простую, среднюю арифметическую взвешенную, среднюю гармоническую взвешенную и т.д.
Продолжительность занятия: 4 часа
Средства обучения: Рабочая тетрадь для практических занятий, калькулятор
Образовательные результаты, заявленные во ФГОС:
Рассчитывать средние величины и показатели вариации;
Понятие о средних величинах и их видах;
Сущность показателей вариации и методику их расчета.
Оценка «5» выставляется, если обучающийся выполнил задание в полной объеме и без ошибок.
Оценка «4» выставляется, если обучающийся выполнил задание в полном объеме, но допустил незначительные ошибки или недочеты.
Оценка «3» выставляется, если имеются ошибки в ходе решения или в результатах решения.
Оценка «2» выставляется, если обучающийся не выполнил предложенные задания.
Предварительная подготовка. Теоретическая справка
Сущность средних величин, виды средних величин, показатели вариации, методика расчета средних величин и показателей
Коммерческий банк выдал в течение года нескольким фирмам пять кредитов:
Размер ссуды, тыс. руб.
Определить средний размер кредита для фирм.
Имеются данные по результатам группировки предприятий по величине капитальных затрат:
Группы предприятий по размеру капитальных затрат, тыс. руб.
Число предприятий в группе
Качество продукции предприятия характеризуется следующими данными (за месяц):
Стоимость бракованной продукции
Определить средний процент брака в целом по предприятию .
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
Размер вклада, руб.
Фирма торгует телевизорами трех классов. В течение дня продано:
Цена телевизора, в долл.
Какова средняя цена телевизоров, проданных фирмой в течение дня?
По следующим данным о распределении 100 рабочих цеха по дневной выработке однотипных изделий определите моду.
Дневная выработка, шт.
Число рабочих, чел
1.Выберите условия, необходимые для расчета средней величины:
А) неоднородность совокупности;
Б) однородность совокупности;
В) достаточный объем совокупности;
Г) большая колеблемость значений показателя.
2. Средняя величина – это:
А) показатель, характеризующий однородность совокупности;
Б) показатель, характеризующий типичный уровень варьирующего признака;
В) показатель, характеризующий частоту вариант.
3. Средняя арифметическая взвешенная применяется в том случае, если:
А) имеется значение признака и неодинаковое значение частоты, с которой встречаются значения признака;
Б) необходимо рассчитать среднее значение темпа роста;
В) значения признака повторяются одинаковое число раз.
4. Модой в ряду распределения является:
А) наибольшая варианта;
Б) варианта, которая чаще всех других встречается;
В) наибольшая частота.
5. Показатели вариации используются для:
А) характеристики динамики явления;
Б) характеристики колеблемости признака и однородности совокупности.
6. Среднее квадратическое отклонение характеризует:
А) среднюю меру отклонений признака от средней величины;
Б) тесноту связи между признаками;
В) однородность совокупности.
7. Среднее значение признака в двух совокупностях одинаково. Может ли быть различной вариация признака в этих совокупностях?
В) нельзя сделать вывод о вариации.
8. Среднее значение признака в двух совокупностях неодинаковы. Может ли быть одинаковой вариация признака в этих совокупностях?
В) вывод сделать нельзя.
Выводы (студент формулирует выводы по всему занятию)
Каковы основные требования к расчету средних величин?
Какие существуют виды средних величин?
Какие существуют показатели вариации?
Добавляйте авторские материалы и получите призы от Инфоурок
Еженедельный призовой фонд 100 000 Р
Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .
- Антонова Олеся ВладимировнаНаписать 1477 01.10.2015
Номер материала: ДВ-023407
Международные дистанционные олимпиады «Эрудит III»
Доступно для всех учеников
1-11 классов и дошкольников
Рекордно низкий оргвзнос
по разным предметам школьной программы (отдельные задания для дошкольников)
Идёт приём заявок
Устанавливая рекомендуемое программное обеспечение вы соглашаетесь
с лицензионным соглашением Яндекс.Браузера и настольного ПО Яндекса .
-
01.10.2015 720
-
01.10.2015 645
-
01.10.2015 1087
-
01.10.2015 818
-
01.10.2015 506
-
01.10.2015 661
-
01.10.2015 846
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Практическое занятие № 3 по теме «Средние значения и вариация»
Цель: освоить расчет средних величин и вариации для анализа данных судебной статистики.
- 1. Рассчитать средний срок лишения свободы по составам преступлений в целом по всем статьям УК РФ, каждой статье и частям УК РФ задания.
- 2. Аналогично рассчитать моду и медиану срока лишения свободы.
- 3. Рассчитать дисперсию срока лишения свободы по каждой статье УК РФ задания.
- 4. Вычислить коэффициент вариации и сделать вывод относительно однородности статистической совокупности.
Исходные статистические данные к заданию представлены в табл. 7. Выбор варианта задания осуществляется в соответствии с табл. 8. Необходимые формулы для расчета приведены в гл. 4 учебника.
Порядок выполнения задания
- 1. Откройте новый файл в программе MS Excel и сохраните файл, указав в имени файла свою фамилию. Создайте в Excel таблицу, подобную табл. 7, оставив в ней только статьи УК РФ, соответствующие вашему варианту. В первой строке вашей таблицы вставьте данные но строке 1 общее число осужденных к лишению свободы по всем статьям УК РФ. Вставьте строки с наименованием статей УК РФ из вашего варианта и просуммируйте в них значения по частям соответствующих статей.
- 2. Добавьте к ней справа семь столбцов: «Средний срок лишения свободы», «Медиана срока лишения свободы», «Мода срока лишения свободы», «Дисперсия срока лишения свободы», «Среднее квадратическое отклонение», «Коэффициент вариации», «Середина ряда» и строку внизу «Середина интервала».
- 3. Определите середины интервалов но всем срокам лишения свободы (х’) и укажите их по графам в строке «Середина интервала». В первом столбце в наименовании столбца — открытый интервал «до 1 года», т.е. не указана нижняя граница. Однако фактически нижняя граница существует — за нее принимается 2 месяца, или 1/6 года, т.е. минимальный срок лишения свободы, определенный в в ст. 56 Общей части УК РФ. Середины интервалов будут являться вариантами х’, а число осужденных, которым назначили соответствующие сроки лишения свободы, — частотами /.
Число осужденных по срокам лишения свободы по распространенным составам преступлений в Российской Федерации в 2013 г. [1]
Число осужденных по с
юкам лишения свободы
До 1 года включительно
Свыше 1 до 2 лет включительно
Свыше 2 до 3 лет включительно
Свыше 3 до 5 лет включительно
Свыше 5 до 8 лет включительно
Свыше 8 до 10 лет включительно
Свыше 10 до 15 лет включительно
Свыше 15 до 20 лет включительно
по составам УК РФ
Число осужденных но срокам лишения свободы
До 1 года включительно
Свыше 1 до 2 лет включительно
Свыше 2 до 3 лет включительно
Свыше 3 до 5 лет включительно
Свыше 5 до 8 лет включительно
Свыше 8 до 10 лет включительно
Свыше 10 до 15 лет включительно
Свыше 15 до 20 лет включительно
Число осужденных по с
юкам лишения свободы
До 1 года включительно
Свыше 1 до 2 лет включительно
Свыше 2 до 3 лет включительно
Свыше 3 до 5 лет включительно
Свыше 5 до 8 лет включительно
Свыше 8 до 10 лет включительно
Свыше 10 до 15 лег включительно
Свыше 15 до 20 лет включительно
Число осужденных по с
юкам лишения свободы
До 1 года включительно
Свыше 1 до 2 лет включительно
Свыше 2 до 3 лет включительно
Свыше 3 до 5 лет включительно
Свыше 5 до 8 лет включительно
Свыше 8 до 10 лет включительно
Свыше 10 до 15 лег включительно
Свыше 15 до 20 лет включительно
4. Вычислите средние сроки лишения свободы по каждой статье вашего варианта (части статьи) УК РФ. Для этого выделите первую свободную ячейку столбца «Средний срок лишения свободы» и после знака «=» задайте в ней формулу расчета средней взвешенной для первой в вашем варианте статьи УК РФ. В данном случае средней арифметической взвешенной будет сумма произведений середин интервалов сроков лишения свободы (варианты х’) на соответствующее им число осужденных (частоту У) но строке для данной статьи УК РФ, деленная на общее число осужденных к лишению свободы по этой статье УК РФ. При вводе формулы не забудьте зафиксировать постоянные адреса ячеек, ссылающиеся на середины интервалов х‘ (ввод признаков постоянной ячейки знаков $ перед именем столбца и строки функциональной клавишей F4).
Формула должна быть введена последовательным умножением варианта на частоту в столбце, их суммированием, и общая сумма разделена на общее число осужденных в строке. Выполнив расчет, убедитесь, что введенные имена ячеек ссылаются на нужные значения (дважды кликните на рассчитанное по формуле значение — отобразится цветное выделение ячеек, на которые ссылается формула). Протяните формулу по всем строкам данного столбца — для всех статей.
Вариант индивидуального задания
- 105,
- 111
- 112,
- 117
- 158,
- 159
- 160,
- 161
- 162,
- 163
- 117,
- 318
- 163,
- 166
- 105,
- 158
Для расчета суммы произведений частоты (количества осужденных) на вес (середина интервала срока лишения свободы) при расчете суммарного срока лишения свободы при желании может использоваться специальная функция сумм производных.
В качестве аргументов функции указывается массив данных 1 — значения по строкам с числом осужденных (/) и массив 2 — значения середины интервалов (.г’).
Не забудьте сумму произведений разделить на общее число осужденных для расчета среднего арифметического взвешенного значения и скобками в формуле определить нужный порядок действий.
- 5. Найдите модальный интервал для числа осужденных по всем строкам (наиболее часто встречающаяся величина — наибольшее число осужденных по срокам лишения свободы). Выделите его цветной заливкой. Рассчитайте значение моды, введя в первую свободную ячейку столбца «Мода срока лишения свободы» после знака «=» формулу для вычисления моды интервального вариационного ряда. Аналогично найдите моду для остальных статей (частей статей) вашего варианта.
- 6. В столбце «Середина ряда» рассчитайте середину ряда — 1/2 от общего числа осужденных к лишению свободы по строке. Найдите медианный интервал для числа осужденных по каждой строке из статей УК РФ (части статьи).
Рекомендации. Вычислите середину ряда, медиану для всех строк, определите ячейку, в какой интервал попадает значение середины ряда. Важно понимать, что означает каждый элемент в формуле. Размер медианного интервала, его нижняя и верхняя границы определяются по наименованию медианного интервала («от число Хх до число Х2»). Вычитание накопленной частоты в формуле удобнее выполнить последовательным вычитанием значений в столбцах, предшествующих столбцу, в котором находится медианный интервал.
Рассчитайте значение медианы, введя в первую свободную ячейку столбца «Медиана срока лишения свободы» после знака «=» формулу для вычисления медианы интервального вариационного ряда. Аналогично найдите медиану для остальных статей (частей статей) вашего варианта.
Рекомендации. Обратите внимание, что если мода или медиана находятся по строкам в разных столбцах, то формулу протягивать нельзя, ее нужно вводить заново, а если копировать, то необходимо откорректировать, сделав ссылку на нужные ячейки.
- 7. Введите в первую свободную ячейку столбца «Дисперсия срока лишения свободы» формулу взвешенной дисперсии после знака «=». При этом лучше использовать рекомендуемую формулу, приведенную в теоретической части, средний срок лишения свободы Т, вычисленный на четвертом этапе работы. Протяните формулу по всем строкам данного столбца — для всех статей (не забудьте зафиксировать адреса ячеек, ссылающиеся на середины интервалов знаком $).
- 8. Найдите среднее квадратическое отклонение а по каждой статье, введя в первую свободную ячейку столбца «Среднее квадратическое отклонение» после знака «=» формулу для его вычисления.
- 9. Найдите коэффициент вариации по каждой статье, введя в первую свободную ячейку столбца «Коэффициент вариации» после знака «=» формулу для его вычисления.
- 10. Сделайте вывод об однородности статистических совокупностей, используя полученные значения коэффициента вариации (более 33% — совокупность считается неоднородной).
И. Постройте диаграммы:
- — отражающую распределение числа осужденных по срокам лишения свободы в целом по всем статьям УК РФ;
- — распределение числа осужденных по статьям УК РФ в вашем варианте в целом по статье и по отдельным частям статьи УК РФ (если в вашем варианте средний срок лишения свободы рассчитывался по нескольким статьям, целесообразно для каждой построить отдельную диаграмму).
Дополнительное задание к практическому занятию № 3
Цель: закрепить навыки расчета средних величин.
- 1. Рассчитайте средние размеры взяток но каждому составу преступления но сводным данным но Российской Федерации за 2014 г. (для расчета используйте данные статистической таблицы «Размеры взяток» из фрагмента формы 10.4.1 по делам коррупционной направленности) 1 . Данные по показателю услуги неимущественного характера из расчета исключите.
- 2. По сводным данным в статистической таблице «Виды наказаний» рассчитайте средний срок реального лишения свободы осужденным за преступления коррупционной направленности. Рассчитайте три вида средних величин: среднюю взвешенную, моду и медиану.
- 3. Рассчитайте средние значения назначенных сумм штрафа в сводной статистической отчетности по строкам формы № 1-АП [2][3] .
Рассчитайте долю взысканных сумм штрафа от наложенных штрафов по вступившим в силу судебным постановлениям.
Рекомендации. С правой стороны формы создайте дополнительный столбец «Средний размер штрафа/суммы, присужденный к взысканию». Введите формулу — для среднего штрафа — ячейку с суммой наложенного штрафа разделите на число оштрафованных лиц. Отфильтруйте значения по возрастанию или поставьте условное форматирование (например, ячейки, содержащие данные больше определенного значения, окрашивать желтой заливкой).
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | |||
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | |||
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.